Rademacher type and Enflo type coincide

Recently we posted a paper on arXiv “Rademacher type and Enflo type coincide” with Ramon van Handel and Alexander Volberg solving an old problem in Banach space theory. The question is to understand under what conditions on a Banach space X we have dimension free Poincare type inequality

\begin{aligned}\mathbb{E} \|f(\varepsilon) - f(-\varepsilon)\|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \| D_{j} f(\varepsilon)\|^{2} \quad \quad (1)\end{aligned}

for all f:\{-1,1\}^{n} \to X and all n \geq 1. Here, C=C(X)<\infty is some universal constant (independent of f and the dimension n of the hypercube \{-1,1\}^{n}), \varepsilon=(\varepsilon_{1}, \ldots, \varepsilon_{n}) \in\{-1,1\}^{n} is uniformly distributed on the Hamming cube \{-1,1\}^{n}, and
\begin{aligned} D_{j}f(\varepsilon) = \frac{f(\varepsilon_{1}, \ldots, \varepsilon_{j}, \ldots, \varepsilon_{n})-f(\varepsilon_{1}, \ldots, -\varepsilon_{j}, \ldots , \varepsilon_{n})}{2} \end{aligned}.

Remark: one can ask the validity of (1) with an arbitrary power p>0, i.e., \mathbb{E} \|f(\varepsilon) - f(-\varepsilon)\|^{p} \leq C \mathbb{E} \sum_{j=1}^{n} \| D_{j} f(\varepsilon)\|^{p} instead of p=2. Notice that if p \in (0,1] then the “triangle inequality” \|x+y\|^{p} \leq \|x\|^{p}+\|y\|^{p} together with telescoping sum
f(\varepsilon)-f(-\varepsilon)=f(\varepsilon_{1},\varepsilon_{2}, \ldots, \varepsilon_{n}) -f(-\varepsilon_{1},\varepsilon_{2}, \ldots, \varepsilon_{n})+f(-\varepsilon_{1},\varepsilon_{2}, \ldots, \varepsilon_{n})-f(-\varepsilon_{1},-\varepsilon_{2}, \ldots, \varepsilon_{n})+...+f(-\varepsilon_{1}, \ldots, -\varepsilon_{n-1}, \varepsilon_{n})-f(-\varepsilon)

trivially implies (1) for any normed space X.

Also notice that if p>2 then testing (1) on
f(\varepsilon_{1},...,\varepsilon_{n}):=x\cdot (\frac{\varepsilon_{1}+...+\varepsilon_{n}}{\sqrt{n}}) for some x \neq 0 implies

\begin{aligned} \mathbb{E} \left|\frac{\varepsilon_{1}+...+\varepsilon_{n}}{\sqrt{n}}\right|^{p} \leq C n^{1-\frac{p}{2}}\end{aligned}.

But by the central limit theorem
\begin{aligned}\mathbb{E} |\frac{\varepsilon_{1}+...+\varepsilon_{n}}{\sqrt{n}}|^{p} \to \int_{\mathbb{R}}|s|^{p} \frac{e^{-s^{2}/2}}{\sqrt{2\pi}}ds=B(p)>0 \end{aligned},

i.e., B(p) < C' n^{1-\frac{p}{2}} for sufficiently large n which is impossible when p>2. Thus no normed space satisfies (1) for p >2.

Therefore, (1) makes nontrivial sense only for p \in (1,2]. Since the solution of the problem that I am going to present does not see any difference between p=2 or p\in (1,2] we will be working only with the case p=2.

It was conjectured that (1) holds for all f :\{-1,1\}^{n}\to X if and only if (1) holds for linear functions only, i.e., f(\varepsilon) = \varepsilon_{1}x_{1}+\ldots+\varepsilon_{n} x_{n}. When f is linear the inequality (1) takes the form

\begin{aligned} \mathbb{E} \| \varepsilon_{1}x_{1}+\ldots+\varepsilon_{n} x_{n}\|^{2} \leq C' \sum_{j=1}^{n} \|x_{j}\|^{2} \quad \quad (2)\end{aligned}
and such Banach spaces which satisfy (2) for all n \geq 1 are called of type-2 (Rademacher type-2). The Banach spaces which satisfy (1) for all f are called of Enflo type-2. Enflo type implies Rademacher type. What about the converse?

Banach spaces of type-2 have several key properties which I won’t have time to discuss today. An interesting part about Enflo type is that it can be written for an arbitrary metric space without using any linear structure as in (2).

Definition.
We say that a metric space (Y, d) has Enflo type-2 if

\begin{aligned} \mathbb{E} d(f(\varepsilon), f(-\varepsilon))^{2} \leq C \mathbb{E} \sum_{j=1}^{n} d(f(\varepsilon_{1}, \ldots, \varepsilon_{j}, \ldots, \varepsilon_{n}), f(\varepsilon_{1}, \ldots, -\varepsilon_{j}, \ldots, \varepsilon_{n}))^{2}\end{aligned}

holds for all f:\{-1,1\}^{n} \to Y and all n \geq 1 with some universal constant C=C(Y)<\infty.

The hope was that maybe Enflo type is the “correct” extension of Rademacher type for metric spaces, and if so then it could be that many good properties that are obtained for Banach spaces under sole assumption of being of Rademacher type can be “transferred” to metric spaces having Enflo type. So this would create a “bridge” between Banach spaces and metric spaces (the subject of “Ribe program”), and even more, one may transfer some techniques from Banach spaces to metric spaces. Therefore, the first open question was whether Enflo type = Rademacher type for Banach spaces.

Let me mention some partial progress.

Theorem 1. (Bourgain–Milman–Wolfson, 1986).
Rademaher type 2 implies Enflo type-2 with constant A(p)n^{2-p} for any p<2.

In other words Theorem-1 says that if \mathbb{E}\|f(\varepsilon) - f(-\varepsilon)\|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \| D_{j} f(\varepsilon)\|^{2} holds for linear functions with some universal constant C<0, then for any p<2, we have \mathbb{E}\|f(\varepsilon) - f(-\varepsilon)\|^{2} \leq A(p) n^{2-p} \mathbb{E} \sum_{j=1}^{n} \| D_{j} f(\varepsilon)\|^{2} holds for all functions f:\{-1,1\}^{n} \to X. We really want to take p=2 but the problem is that A(p) becomes infinity at p=2.

Theorem 2. (Pisier, 1986) If Banach space has Rademacher type -2 then \mathbb{E} \|f(\varepsilon) - f(-\varepsilon)\|^{q} \leq B(q) \mathbb{E} \sum_{j=1}^{n} \| D_{j} f(\varepsilon)\|^{q} holds for all q<2, i.e., X has Enflo type-q for any q<2.

The constant B(q) becomes infinity at q=2. Pisier was interested in the inequality \mathbb{E} \| f(\varepsilon) - \mathbb{E}f\|^{2} \leq C \mathbb{E} \| \sum_{j=1}^{n} \delta_{j} D_{j}f(\varepsilon) \|^{2} where in the right hand side the expectation is taken with respect to independent identically distributed uniform \delta = (\delta_{1}, \ldots, \delta_{n}), \varepsilon = (\varepsilon_{1}, \ldots, \varepsilon_{n}) \in \{-1,1\}^{n}. If we would’ve had such inequality then (using Rademacher type -2) we could write

\begin{aligned}\mathbb{E} \| \sum_{j=1}^{n} \delta_{j} D_{j}f(\varepsilon) \|^{2} =\mathbb{E}_{\varepsilon} \mathbb{E}_{\delta} \| \sum_{j=1}^{n} \delta_{j} D_{j}f(\varepsilon) \|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \|D_{j} f(\varepsilon)\|^{2}\end{aligned}

and this would give us Enflo type-2 (using an obvious inequality \mathbb{E} \|f(\varepsilon) - f(-\varepsilon)\|^{2} \leq 4 \mathbb{E} \| f - \mathbb{E}f\|^{2})
But the problem was that Pisier proved his inequality with logarithmic term, i.e.,

\begin{aligned} \mathbb{E} \| f - \mathbb{E}f\|^{2} \leq 10 \log(n) \mathbb{E} \| \sum_{j=1}^{n} \delta_{j} D_{j}f(\varepsilon) \|^{2} \quad (3)\end{aligned},

This gives Enflo type -2 with constant C \approx \log(n). One may hope to remove \log(n) in Pisier’s inequality (3) but unfortunately this not possible.

Theorem 3.(Talagrand, 1993) There exists a Banach space X for which \log(n) factor in Pisier’s inequality (3) is optimal.

Talagrand’s example is kind of mysterious in a sense that it reminds me when a magician pulls a rabbit out of a hat. But is it really so? I am planning to talk about it in another post.

Important partial results have been obtained under stronger assumptions than Rademacher type 2: \mathrm{UMD} and Rademacher type imply Enflo type (Naor–Schechtman); \mathrm{UMD}^{+} for X^{*}, and Rademacher type for X imply Enflo type (Naor–Hytonen); Rademacher type implies Scaled Enflo type (Mendel–Naor); relaxed UMD property and Rademacher type imply Enflo type (A. Eskenazis); superreflexivity and Rademacher type imply Enflo type with constant C \sim \log^{\alpha}(n) for some \alpha \in (0,1) (Naor–Eskenazis).

We are going to prove

Theorem: Rademacher type and Enflo type coincide.

Proof. Assume X is of Rademacher type 2, i.e., we have \mathbb{E} ||\sum_{j=1}^{n} \varepsilon_{j} x_{j} \|^{2} \leq C \sum_{j=1}^{n} \|x_{j}\|^{2} with some universal constant. Due to an obvious inequality (a+b)^{2} \leq 2a^{2}+2b^{2} we have
\mathbb{E} \| f(\varepsilon) - f(-\varepsilon)\|^{2} =\mathbb{E} \| f(\varepsilon) - \mathbb{E}f + \mathbb{E} f - f(-\varepsilon) \|^{2} \leq 4 \mathbb{E} \|f(\varepsilon) - \mathbb{E} f\|^{2}. Thus it suffices to prove the Poincare inequality

\begin{aligned} \mathbb{E} \|f-\mathbb{E} f\|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \|D_{j} f\|^{2} \quad \text{for all} \quad f:\{-1,1\}^{n} \to X\end{aligned}

Any function f :\{-1,1\}^{n} \to X we can decompose into Fouirer–Walsh series

\begin{aligned}f(\varepsilon) = \sum_{S \subset \{1, \ldots, n\}}a_{S} \prod_{j \in S} \varepsilon_{j} \quad \text{with} \quad a_{S} \in X\end{aligned}.

Next, consider the Hermite operator

\begin{aligned} T_{r}f(\varepsilon) =\sum_{S \subset \{1,\ldots, n\}} r^{|S|}a_{S}\prod_{j \in S} \varepsilon_{j}, \quad r \in \mathbb{R}\end{aligned}

Notice that T_{0}f = \mathbb{E}f, and T_{1}f = f. Therefore, we can interpolate

\begin{aligned} f - \mathbb{E}f = \int_{0}^{1}\frac{d}{dr}T_{r}f dr \end{aligned}.

Next, we have

\begin{aligned}\frac{d}{dr}T_{r}f = \sum_{S \subset \{1, \ldots, n\}} |S| r^{|S|-1} a_{S}\prod_{j \in S} \varepsilon_{j}\end{aligned}.

If we define the laplacian as \Delta f = \sum_{j=1}^{n} D_{j} f then, obviously, \Delta \prod_{j\in S} \varepsilon_{j} = |S| \prod_{j \in S} \varepsilon_{j}. Thus by linearity we have \frac{d}{dr} T_{r} f = \frac{1}{r} \Delta T_{r} f = \frac{1}{r} T_{r} \Delta f. It is not hard to see that for any g :\{-1,1\}^{n} \to X^{*}, where X^{*} is dual to X we have integration by parts formula

\mathbb{E}\langle g, \Delta f \rangle = \mathbb{E} \sum_{j=1}^{n} \langle D_{j} g, D_{j} f \rangle. Therefore, if we let \| f\|_{L^{2}(X)} := (\mathbb{E} \|f\|^{2})^{1/2} we obtain

\begin{aligned}\| f-\mathbb{E}f \|_{2} = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \mathbb{E} \langle g(\varepsilon), f(\varepsilon)-\mathbb{E}f \rangle = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \mathbb{E} \left\langle g(\varepsilon), \int_{0}^{1} \frac{d}{dr} T_{r} f(\varepsilon) dr \right\rangle \end{aligned}
\begin{aligned} = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\mathbb{E} \left\langle g(\varepsilon), \frac{1}{r}\Delta T_{r} f(\varepsilon) \right\rangle dr = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\mathbb{E} \sum_{j=1}^{n}\left\langle \frac{1}{r}D_{j}T_{r}g(\varepsilon),D_{j}f(\varepsilon) \right\rangle dr. \end{aligned}

Next, let us have a close look at \frac{1}{r}D_{j} T_{r} g(\varepsilon). Define i.i.d. random variables

\begin{aligned} \xi_{j} = \begin{cases} 1 & \text{with probability} \quad \frac{1+r}{2}, \\ -1 & \text{with probability} \quad \frac{1-r}{2} \end{cases} \end{aligned}

for any r \in (0,1), and all j=1, \ldots, n. Let \xi = (\xi_{1}, \ldots, \xi_{n}), and let \xi \varepsilon = (\xi_{1} \varepsilon_{1}, \ldots, \xi_{n} \varepsilon_{n}). It is clear that \mathbb{E}_{\xi} g(\xi \eta) = T_{r} g(\varepsilon) just because \mathbb{E}_{\xi} \xi_{j} =r, and hence \mathbb{E}_{\xi} \prod_{j\in S} \xi_{j} = r^{|S|}. Next, let us calculate D_{k} \mathbb{E}_{\xi} g(\xi \varepsilon). We have

\begin{aligned}\mathbb{E}_{\xi} g(\xi_{1} \varepsilon_{1}, \ldots, \xi_{n} \varepsilon_{n}) = \sum_{\eta \in \{-1,1\}^{n}} g(\eta_{1} \varepsilon_{1}, \ldots, \eta_{n} \varepsilon_{n}) \prod_{j=1}^{n} \left(\frac{1+\eta_{j} r}{2}\right).\end{aligned}

\begin{aligned} \mathbb{E}_{\xi} g(\xi_{1} \varepsilon_{1}, \ldots,-\xi_{k} \varepsilon_{k}, \ldots, \xi_{n} \varepsilon_{n}) = \sum_{\eta \in \{-1,1\}^{n}} g(\eta_{1} \varepsilon_{1}, \ldots, -\xi_{k}\varepsilon_{k}, \ldots, \eta_{n} \varepsilon_{n}) \prod_{j=1}^{n} \left(\frac{1+\eta_{j} r}{2}\right) = \end{aligned}

\begin{aligned}\sum_{\eta \in \{-1,1\}^{n}} g(\eta_{1} \varepsilon_{1}, \ldots,\xi_{k} \varepsilon_{k}, \ldots, \eta_{n} \varepsilon_{n}) \left( \frac{1-\eta_{k}r}{1+\eta_{k}r}\right)\prod_{j=1}^{n} \left(\frac{1+\eta_{j} r}{2}\right) \end{aligned}

Therefore

\begin{aligned} \frac{1}{r}D_{k} \mathbb{E}_{\xi} g(\xi \varepsilon) =\sum_{\eta \in \{-1,1\}^{n}} \left(\frac{\eta_{k}}{1+\eta_{k} r}\right)g(\eta_{1} \varepsilon_{1}, \ldots, \eta_{n} \varepsilon_{n}) \prod_{j=1}^{n} \left(\frac{1+\eta_{j} r}{2}\right) =\mathbb{E}_{\xi} \delta_{k}(\xi) g(\xi \varepsilon)\end{aligned}

where \begin{aligned} \delta_{k}(\xi) := \frac{\xi_{k} }{1+\xi_{k} r} \end{aligned}. Therefore we can proceed as

\begin{aligned} \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\mathbb{E} \sum_{j=1}^{n}\left\langle \frac{1}{r} D_{j}T_{r}g(\varepsilon), D_{j}f(\varepsilon) \right\rangle dr = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\mathbb{E}_{\xi, \varepsilon} \sum_{j=1}^{n}\left\langle \delta_{j}(\xi)g(\xi \varepsilon), D_{j}f(\varepsilon) \right\rangle dr \end{aligned}

\begin{aligned} = \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\mathbb{E}_{\xi, \varepsilon} \left\langle g(\xi \varepsilon), \sum_{j=1}^{n} \delta_{j}(\xi)D_{j}f(\varepsilon) \right\rangle dr \end{aligned}

\begin{aligned} \leq \sup_{\| g\|_{L^{2}(X^{*})}\leq 1} \int_{0}^{1}\left(\mathbb{E}_{\xi, \varepsilon}\| g(\xi \varepsilon)\|^{2} \right)^{1/2}\left( \mathbb{E}_{\xi, \varepsilon}\left \| \sum_{j=1}^{n} \delta_{j}(\xi) D_{j}f(\varepsilon) \right\|^{2} \right)^{1/2} dr \end{aligned}

\begin{aligned} = \int_{0}^{1}\left( \mathbb{E}_{\xi, \varepsilon}\left \| \sum_{j=1}^{n} \frac{\xi_{j}}{1+\xi_{j} r} D_{j}f(\varepsilon) \right\|^{2} \right)^{1/2} dr \end{aligned}

where we used the fact that \mathbb{E}_{\varepsilon} \|g(\varepsilon)\|^{2} = \mathbb{E}_{\xi, \varepsilon} \|g(\xi \varepsilon)\|^{2}.

Thus at this moment for any Banach space X we have proved

\begin{aligned} \| f-\mathbb{E} f\|_{2} \leq \int_{0}^{1}\left( \mathbb{E}_{\xi, \varepsilon}\left \| \sum_{j=1}^{n} \frac{\xi_{j}}{1+\xi_{j} r} D_{j}f(\varepsilon) \right\|^{2} \right)^{1/2} dr \quad (5)\end{aligned}

(the reader should compare it to Pisier’s inequality (3)).

Now it is a simple application of a standard symmetrization technique to complete the proof of the theorem from (5). Indeed, let \xi', \varepsilon' be independent copies of \xi, \varepsilon correspondingly. Let r \in (0,1). Notice that

\begin{aligned} \mathbb{E}_{\xi} \frac{\xi_{j}}{1+\xi_{j} r} =0. \end{aligned}.

Therefore, by convexity we have

\begin{aligned} \mathbb{E}_{\xi, \varepsilon}\left \| \sum_{j=1}^{n} \left( \frac{\xi_{j}}{1+\xi_{j} r}\right)D_{j}f(\varepsilon) \right\|^{2} \leq \mathbb{E}_{\xi, \varepsilon, \xi'}\left \| \sum_{j=1}^{n} \left( \frac{\xi_{j}}{1+\xi_{j} r} - \frac{\xi'_{j}}{1+\xi'_{j} r}\right)D_{j}f(\varepsilon) \right\|^{2} \end{aligned}

\begin{aligned} = \mathbb{E}_{\xi, \varepsilon, \xi', \varepsilon' }\left \| \sum_{j=1}^{n} \varepsilon'_{j}\left( \frac{\xi_{j}}{1+\xi_{j} r} - \frac{\xi'_{j}}{1+\xi'_{j} r}\right)D_{j}f(\varepsilon) \right\|^{2} \leq C \mathbb{E}_{\xi, \varepsilon, \xi'} \sum_{j=1}^{n} \left( \frac{\xi_{j}}{1+\xi_{j} r} - \frac{\xi'_{j}}{1+\xi'_{j} r}\right)^{2} \left \|D_{j}f(\varepsilon) \right\|^{2}.\end{aligned}

Thus

\begin{aligned}\mathbb{E} \| f-\mathbb{E}f \|^{2} \leq C \left(\int_{0}^{1} \left( \mathbb{E}_{\xi, \xi'}\left|\frac{\xi_{1}}{1+\xi_{1} r} - \frac{\xi'_{1}}{1+\xi'_{1} r} \right|^{2} \right)^{1/2} dr \right)^{2} \mathbb{E} \sum_{j=1}^{n}\left \|D_{j}f(\varepsilon) \right\|^{2}. \end{aligned}

And the calculus shows

\begin{aligned} \left(\int_{0}^{1} \left( \mathbb{E}_{\xi, \xi'}\left|\frac{\xi_{1}}{1+\xi_{1} r} - \frac{\xi'_{1}}{1+\xi'_{1} r} \right|^{2} \right)^{1/2} dr \right)^{2} =2\left( \int_{0}^{1} \frac{dr}{\sqrt{1-r^{2}}}\right)^{2} = \frac{\pi^{2}}{2}. \end{aligned}

This finishes the proof of the theorem \square.

UPDATE 4.2.2021:
There seems to be an interesting historical background about this problem, see, for example, Per Enflo’s blog. See also this blog for a very nice exposition about Enflo’s problem. Here is the recorded talk I gave at Corona seminar.

8 thoughts on “Rademacher type and Enflo type coincide”

  1. Dear Paata,

    Thank you very much for the amazing paper and for the post! Quick question: is it easy to see whether your dimension-free Poincare-type inequality implies Pisier’s (log n)-factor inequality, which has Rademachers instead of your “standardized biased Rademachers”?

    Like

    Reply

    1. Dear Anon,

      Thank you for the question, this was also mentioned to me by Alexandros Eskenazis. Pisier’s inequality can be obtained from this argument by integrating over the interval [0,s] instead of [0,1] where s = 1-\frac{1}{n}. Indeed, starting with 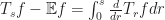T_{s}f-\mathbb{E}f = \int_{0}^{s}\frac{d}{dr}T_{r}fdr the inequality (5) takes the form (here p=2) \|T_{s}f-\mathbb{E}f\|_{p} \leq \int_{0}^{s}\left(\mathbb{E}_{\xi, \varepsilon}\left\| \sum_{j=1}^{n} \frac{\xi_{j}}{1+\xi_{j}r}D_{j}f(\varepsilon)\right\|^{p}\right)^{1/p}dr. Now the integrand in the right hand side by Kahan’s contraction principle can be estimated as \max \left|\frac{\xi_{1}}{1+r\xi_{1}}-\frac{\xi'_{1}}{1+r\xi'_{1}}\right| \left( \mathbb{E}_{\delta, \varepsilon} \| \sum \delta_{j} D_{j} f(\varepsilon)\|^{p}\right)^{1/p} where \delta_{j} are independent copies for \varepsilon_{j}. On the other hand \left|\frac{\xi_{1}}{1+r\xi_{1}}-\frac{\xi'_{1}}{1+r\xi'_{1}}\right| \leq\frac{2}{1-r^{2}}, here \xi'_{1} is independent copy of \xi_{1}. So \int_{0}^{1-1/n}\frac{1}{1-r^{2}}dr \approx \log(n). 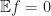In the left hand side we can assume without loss of generality that \mathbb{E}f=0. The claim is that \|T_{1-\frac{1}{n}}f\|_{p}\geq C \|f\|_{p} with some universal constant. 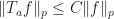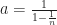Indeed, It suffices to show \|T_{a}f\|_{p}\leq C \|f\|_{p} where a= \frac{1}{1-\frac{1}{n}}. 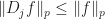Since \|D_{j} f\|_{p}\leq \|f\|_{p} therefore by several application of triangle inequality \|\Delta f\|_{p}\leq n \|f\|_{p}. Thus \|T_{a}f\|_{p}=\|e^{\ln(a)\Delta}f\|_{p}\leq \|\sum_{k=0}^{\infty}\frac{\ln^{k}(a)}{k!}\Delta^{k} f\|_{p}\leq e^{n \ln(a)}\|f\|_{p}\leq C\|f\|_{p}.

      Like

      Reply

      1. Thank you so much for your response, this is great! Despite this last bit, this seems to give a slightly cleaner proof than Pisier’s original argument

        Like

  2. Hi,

    Thanks for the nice exposition. I became aware of this wonderful work through Ramon’s talk last week and it is really nice knowing this. I was trying to think how much can one extend the proof of Poincare inequality for real-valued functions which proceeds more easily by just using the orthonormality of the Fourier-Walsh series and the explicit expressions for the difference operators. It seems this works well for Hilbert spaces as well. Is that right ?

    Liked by 1 person

    Reply

    1. Dear Yogesh,

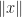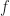      That is right. As long as the norm \| x\| is defined in terms of an inner product \| x\|^{2} = \langle x, x \rangle the standard proof of Poincare inequality \mathbb{E} \| f - \mathbb{E} f\|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \| D_{j} f\|^{2}, i.e., opening the parentheses and using orthogonality, works well. In particular, this covers Hilbert space valued functions f. When we have no information about the norm \| \cdot \| (only the fact that it satisfies triangle inequality) then this “orthogonality” approach does not work anymore, and one has to invent some new techniques. 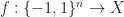As one can see from the proof (Rademacher VS Enflo) in general case the Poincare inequality holds for all f : \{-1,1\}^{n} \to X if and only if 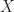X has Rademacher type 2, i.e., \mathbb{E} \| \varepsilon_{1} x_{1}+\ldots+\varepsilon_{n} x_{n}\|^{2} \leq C \sum_{j=1}^{n} \| x_{j}\|^{2}. 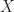Verification of Rademacher type-2 for Hilbert space is easy, we just open the parentheses and use orthogonality, and in general spaces X, other than Hilbert, one needs to invoke some other arguments.

      I also want to mention that for Hilbert space valued functions we have the identity \mathbb{E} \| f - \mathbb{E} f\|^{2} = \mathbb{E} \|f\|^{2} - \|\mathbb{E} f\|^{2}, and sometimes one writes the Poincare inequality as follows \mathbb{E} \|f\|^{2} - \|\mathbb{E} f\|^{2} \leq C \mathbb{E} \sum_{j=1}^{n} \| D_{j} f\|^{2}. 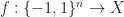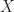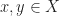However, it is not difficult to show (using induction on the dimension of the Hamming cube \{-1,1\}^{n}) that the “second version” of Poincare inequality holds for Banach space valued functions f : \{-1,1\}^{n} \to X if and only if the space X is 2-uniformly smooth, i.e., \frac{\|x\|^{2}+\|y\|^{2}}{2} - \left\|\frac{x+y}{2}\right\|^{2} \leq C \left\|\frac{x-y}{2}\right\|^{2} holds for all x,y \in X. Now 2-smoothness property implies Rademacher type -2 but not the vise versa. So as long as we change the question a little bit which on the level of Hilbert spaces does not see any difference, the answer can change for Banach spaces.

      Liked by 1 person

      Reply

      1. Dear Paata, Thanks a lot for the detailed explanation and additional remarks. This was very helpful.

        Like

  4. Pingback: Several results on the Hamming cube under one identity – Zeros and Ones

Leave a comment

Design a site like this with WordPress.com
Get started